45. Jump Game II

• categories: Code, Interview Question, leetcode, Medium
• source: https://leetcode.com/problems/jump-game-ii
• topics: Dynamic Programming, Greedy

You are given a 0-indexed array of integers nums of length n. You are initially positioned at nums[0].

Each element nums[i] represents the maximum length of a forward jump from index i. In other words, if you are at nums[i], you can jump to any nums[i + j] where:

• 0 <= j <= nums[i] and
• i + j < n

Return the minimum number of jumps to reach nums[n - 1]. The test cases are generated such that you can reach nums[n - 1].

Left to right with memo and skipped indices

class Solution:
    def jump(self, nums: List[int]) -> int:
        memo = [float(inf)] * len(nums)
        skipped = set()
        memo[0] = 0
        for i in range(len(nums)-1):
            if i in skipped:
                continue
            for j in range(i+1, min(len(nums), i + nums[i] + 1)):
                if nums[j] <= nums[i] - (j - i):
                    skipped.add(j)
                memo[j] = min(memo[j], memo[i] + 1)
        return memo[len(nums) - 1]

Greedy with max reachable index update

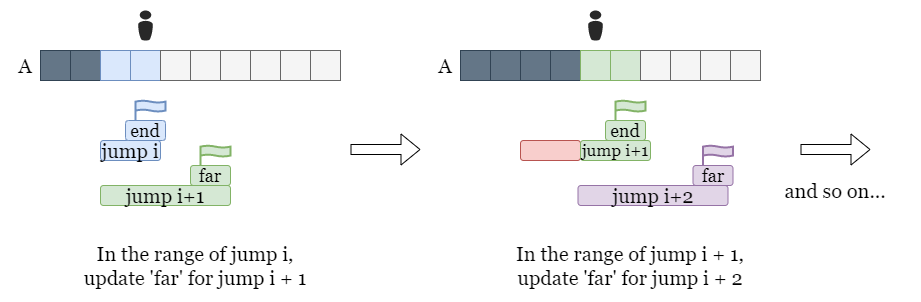
class Solution:
    def jump(self, nums: List[int]) -> int:
        # The starting range of the first jump is [0, 0]
        answer, n = 0, len(nums)
        cur_end, cur_far = 0, 0
 
        for i in range(n - 1):
            # Update the farthest reachable index of this jump.
            cur_far = max(cur_far, i + nums[i])
 
            # If we finish the starting range of this jump,
            # Move on to the starting range of the next jump.
            if i == cur_end:
                answer += 1
                cur_end = cur_far
 
        return answer