Singular Value Decomposition (SVD)

• categories: Linear algebra, Factorization

Definition
The Singular Value Decomposition (SVD) of a matrix $A\in {\mathbb{R}}^{m\times n}$ is a factorization of the form:
$A=U\Sigma V^{\top },$
where:

• $U\in {\mathbb{R}}^{m\times m}$ is an Orthogonal matrix whose columns are the left singular vectors of $A$.
• $\Sigma \in {\mathbb{R}}^{m\times n}$ is a diagonal matrix with non-negative real numbers, called singular values, arranged in descending order.
• $V\in {\mathbb{R}}^{n\times n}$ is an Orthogonal matrix whose columns are the right singular vectors of $A$.

Construction
SVD is derived by observing the properties of $A^{\top }A$ and $A{A}^{\top }$:

1. $A^{\top }A\in {\mathbb{R}}^{n\times n}$ and $A{A}^{\top }\in {\mathbb{R}}^{m\times m}$ are symmetric and e.
2. These matrices can be eigen-decomposed as: positive semidefinite $A^{\top }A=V\Lambda V^{\top },A{A}^{\top }=U\Lambda U^{\top },$
   where $\Lambda$ is a diagonal matrix containing eigenvalues.
3. The singular values of $A$ are ${\sigma }_i=\sqrt{{\lambda }_i}$, where ${\lambda }_i$ are the eigenvalues of $A^{\top }A$ or $A{A}^{\top }$.

Intuition
The SVD of a matrix can be thought of as a sequence of linear transformations:

1. Rotation (via $V$): Aligns the data to principal directions.
2. Stretching/Squashing (via $\Sigma$): Scales the aligned data along principal directions.
3. Rotation (via $U$): Maps the scaled data to the target space.

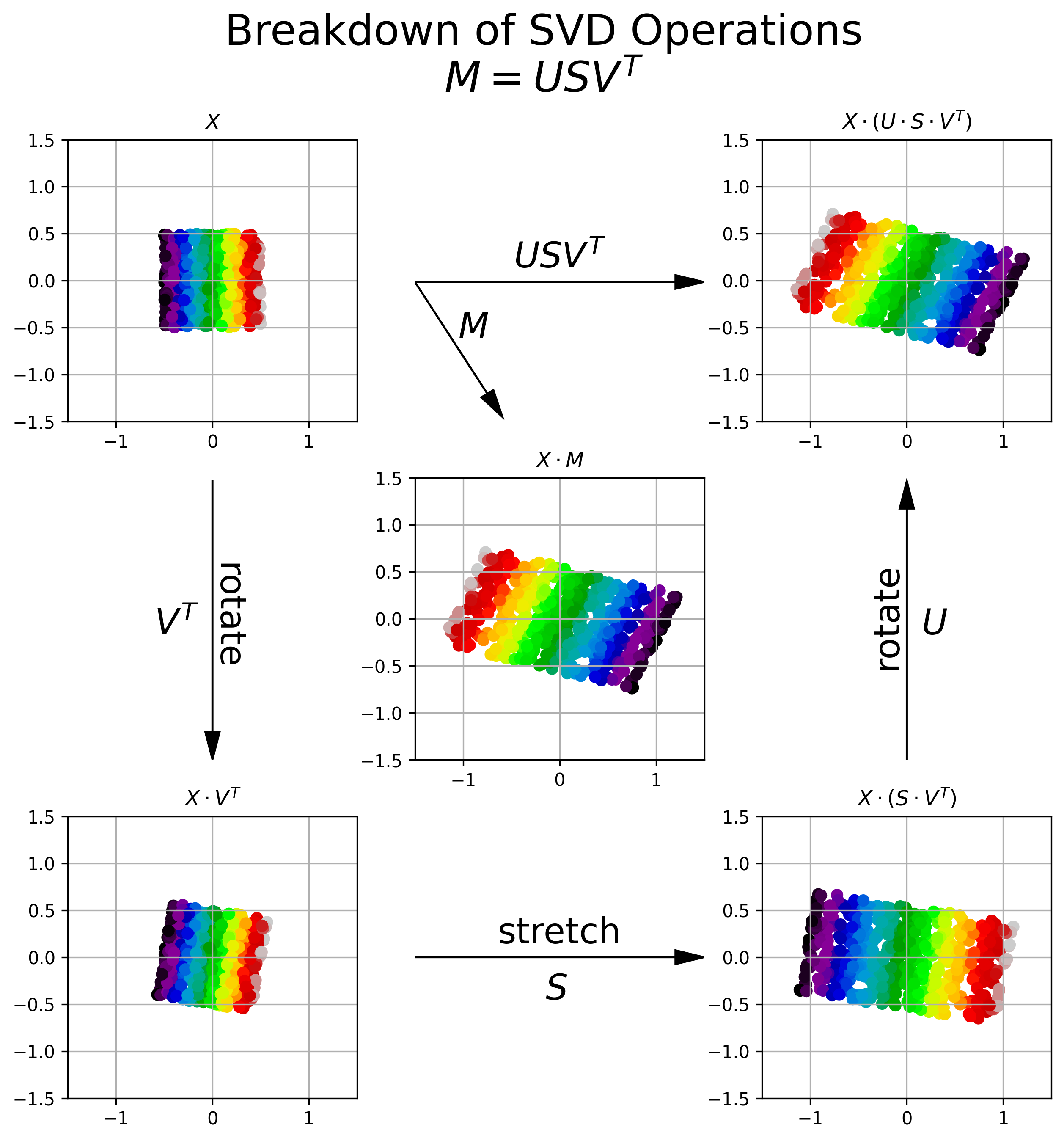
Key Properties

1. Singular Values: The diagonal entries of $\Sigma$ are the singular values ${\sigma }_1\ge {\sigma }_2\ge \cdots \ge 0$.
2. Rank: The rank of $A$ is equal to the number of non-zero singular values.
3. Norms:
   • $\Vert A{\Vert }_F=\sqrt{\sum {\sigma }_i^2}$ (Frobenius Norm).
   • $\Vert A{\Vert }_2={\sigma }_1$ (Spectral Norm).
4. Relation to Eigenvalues: The non-zero eigenvalues of $A^{\top }A$ (or $A{A}^{\top }$) are the squares of the singular values of $A$.

Applications

• Dimensionality Reduction: Core of principal component analysis (PCA).
• Image Compression: Approximates images with low-rank matrices.
• Recommender Systems: Latent factor analysis in collaborative filtering.
• Numerical Solutions: Solving Linear Systems, pseudoinverse computation.
• Data Science: Low-rank approximations for noise reduction.