918. Maximum Sum Circular Subarray

• categories: Code, Interview Question, leetcode, Medium
• source: https://leetcode.com/problems/maximum-sum-circular-subarray
• topics: Kadane’s Algorithm, Array

Description

Given a circular integer array nums of length n, return the maximum possible sum of a non-empty subarray of nums.

A circular array means the end of the array connects to the beginning of the array. Formally, the next element of nums[i] is nums[(i + 1) % n] and the previous element of nums[i] is nums[(i - 1 + n) % n].

A subarray may only include each element of the fixed buffer nums at most once. Formally, for a subarray nums[i], nums[i + 1], ..., nums[j], there does not exist i <= k1, k2 <= j with k1 % n == k2 % n.

Idea

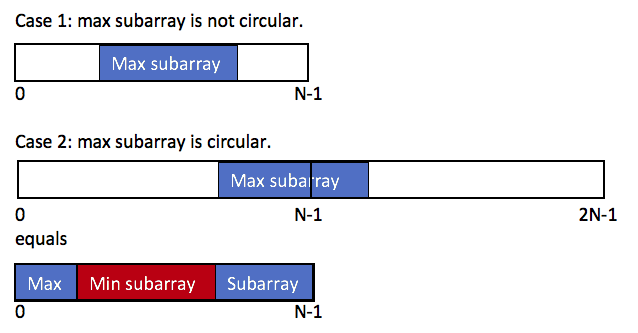
Use Kadane’s algorithm. Find total sum, max and min sub arrays in one iteration, then take the max of max subarray and total - min sub array

Code

class Solution:
    def maxSubarraySumCircular(self, nums: List[int]) -> int:
        current_sum, current_min, total = 0, 0, 0
        best_sum, best_min = float('-inf'), float('inf')
        for a in nums:
            current_sum = max(a, current_sum + a)
            best_sum = max(current_sum, best_sum)
            current_min = min(a, current_min + a)
            best_min = min(best_min, current_min)
            total += a
        
        if total != best_min:
            best_sum = max(best_sum, total - best_min)
            
        return best_sum