- categories: Linear algebra, Factorization
Definition
The Singular Value Decomposition (SVD) of a matrix is a factorization of the form:
where:
- is an Orthogonal matrix whose columns are the left singular vectors of .
- is a diagonal matrix with non-negative real numbers, called singular values, arranged in descending order.
- is an Orthogonal matrix whose columns are the right singular vectors of .
Construction
SVD is derived by observing the properties of and :
- and are symmetric and e.
- These matrices can be eigen-decomposed as: positive semidefinite
where is a diagonal matrix containing eigenvalues. - The singular values of are , where are the eigenvalues of or .
Intuition
The SVD of a matrix can be thought of as a sequence of linear transformations:
- Rotation (via ): Aligns the data to principal directions.
- Stretching/Squashing (via ): Scales the aligned data along principal directions.
- Rotation (via ): Maps the scaled data to the target space.
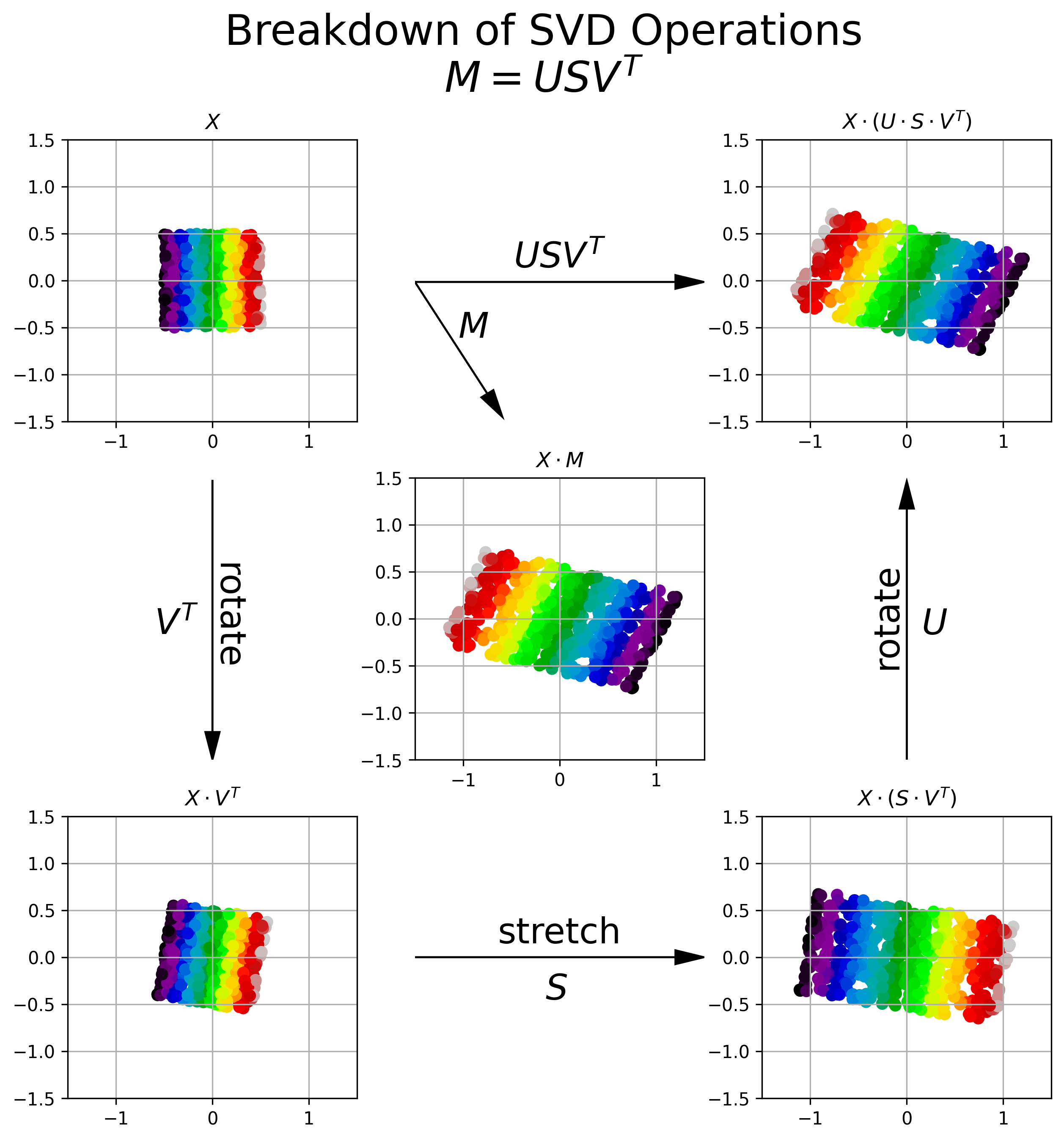
Key Properties
- Singular Values: The diagonal entries of are the singular values .
- Rank: The rank of is equal to the number of non-zero singular values.
- Norms:
- (Frobenius Norm).
- (Spectral Norm).
- Relation to Eigenvalues: The non-zero eigenvalues of (or ) are the squares of the singular values of .
Applications
- Dimensionality Reduction: Core of principal component analysis (PCA).
- Image Compression: Approximates images with low-rank matrices.
- Recommender Systems: Latent factor analysis in collaborative filtering.
- Numerical Solutions: Solving Linear Systems, pseudoinverse computation.
- Data Science: Low-rank approximations for noise reduction.