Moore–Penrose Inverse

• categories: Linear algebra, Matrix

Definition

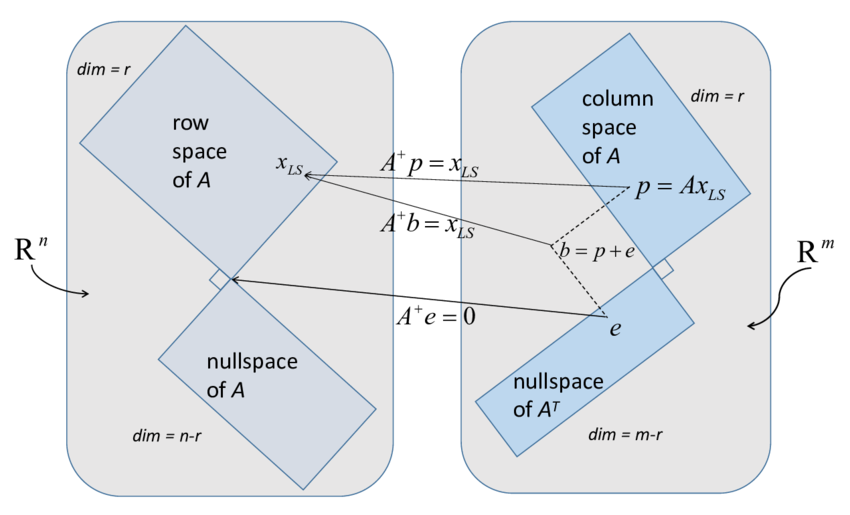
The Moore–Penrose inverse of a matrix $A\in {\mathbb{R}}^{m\times n}$, denoted $A^{+}$, is a generalized inverse that satisfies specific conditions. It is particularly useful for solving Least Squares Problems and Linear Systems equations when $A$ is not square or not invertible.

Conditions for $A^{+}$

The Moore–Penrose inverse $A^{+}$ is the unique matrix that satisfies the following four conditions:

1. Reflexivity:

   $$A{A}^{+}A=A.$$

2. Symmetry:

   $$A^{+}A{A}^{+}=A^{+}.$$

3. Hermitian Property for $A{A}^{+}$:

   $$(A{A}^{+}{)}^T=A{A}^{+}.$$

4. Hermitian Property for $A^{+}A$:

   $$(A^{+}A{)}^T=A^{+}A.$$

If $A$ is a real matrix, the transpose $(\cdot {)}^T$ is used; for complex matrices, the conjugate transpose $(\cdot {)}^H$ applies.

---

Computing the Moore–Penrose Inverse

1. Singular Value Decomposition (SVD)

The most common method to compute $A^{+}$ is via the SVD. If $A\in {\mathbb{R}}^{m\times n}$ has an SVD:

$$A=U\Sigma V^T,$$

where:

• $U\in {\mathbb{R}}^{m\times m}$ and $V\in {\mathbb{R}}^{n\times n}$ are orthogonal matrices,
• $\Sigma \in {\mathbb{R}}^{m\times n}$ is a diagonal matrix of singular values ${\sigma }_1,{\sigma }_2,\dots$,

then the Moore–Penrose inverse is:

$$A^{+}=V{\Sigma }^{+}{U}^T,$$

where ${\Sigma }^{+}\in {\mathbb{R}}^{n\times m}$ is formed by:

• Replacing each non-zero singular value ${\sigma }_i$ in $\Sigma$ with its reciprocal $\frac{1}{{\sigma }_i}$,
• Transposing $\Sigma$.

---

2. Least-Squares Solution

The Moore–Penrose inverse provides the least-squares solution to $A\mathbf{x}=\mathbf{b}$:

$$\mathbf{x}=A^{+}\mathbf{b}.$$

---

Properties

1. Symmetry for Symmetric Matrices:
   If $A$ is symmetric, $A^{+}$ is also symmetric:

   $$(A^{+}{)}^T=A^{+}.$$

2. Consistency with Regular Inverse:
   If $A$ is square and invertible, then:

   $$A^{+}=A^{-1}.$$

3. Rank Property:
   If $A$ has rank $r$, then:

   $$\text{rank}(A^{+})=\text{rank}(A)=r.$$

4. Idempotence:
   The products $A{A}^{+}$ and $A^{+}A$ are idempotent:

   $$(A{A}^{+}{)}^2=A{A}^{+},(A^{+}A{)}^2=A^{+}A.$$

5. Orthogonal Projections:
   $A{A}^{+}$ and $A^{+}A$ are orthogonal projection matrices:

   • $A{A}^{+}$ projects onto the column space of $A$.
   • $A^{+}A$ projects onto the row space of $A$.

---

Applications

1. Solving Linear Systems:

   • Exact solutions: If $A\mathbf{x}=\mathbf{b}$ is consistent, the solution is: $$\mathbf{x}=A^{+}\mathbf{b}.$$
   • Least-squares solutions: For inconsistent systems: $$\mathbf{x}=A^{+}\mathbf{b}\text{minimizes }\Vert A\mathbf{x}-\mathbf{b}{\Vert }_2.$$

2. Matrix Approximation: The Moore–Penrose inverse is used in low-rank approximations, such as in data compression and signal processing.

3. Control Theory: Used in pseudo-inversion of non-square matrices in systems with more equations than unknowns or vice versa.

4. Machine Learning: Regularized least-squares regression uses the Moore–Penrose inverse to compute weights.